注: 这个问题来自China Theory Week 2008的 Open Problems Session。
我们知道在数学里证明一个东西的存在性的时候,有时候只证明了「存在性」,而且在证明过程中并没有说明如何找到它,这种证明方法被称为「非构造性证明」。有些流派的数学家对这种证明方法非常不满,具体这里就不详谈了。
这里要说的是,一个玩意儿,即时你知道它总是存在的,它也是可以算出来的,但是不是就一定能够很快的比如在多项式时间之内算出来呢?
Game Theory已经证明了在两人非合作博弈中,纳什均衡总是存在的,但是如何计算它确被证明是 PPAD-hard的,一个被猜测不属于 P 的复杂类。
纳什均衡的计算问题不太好理解,下面介绍一个问题,描述比较简单非常容易理解。它有类似的效果,存在性可在数学上被证明,但如何计算它却不知道,复杂性也未知。
输入:一个$ 3n$ 点的图,顶点构成一个正$ 3n$ 边形,以及它们之间的$ 6n$ 条边。其中$ 3n$ 条为多边形的边,另外$ 3n$ 条边构成$ n$ 个顶点互不重合的三角形。下图为一个$ n=3$ 的例子。
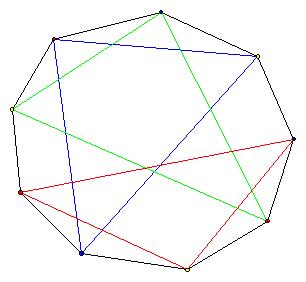
输出:这个图的一种三染色方案(给定点染色,使任何有边相连的顶点都不同色)。
Q. E. D.
