【提示: GIF 动画图片较大,有时需等会儿才能显示动画效果。】
最近人人网上流行一个神奇的椭圆,有不少同学给了不同的扩展。我把看到的在这里总结一下。
这个「神奇的椭圆」最早应该是来自 Cornell 大学的一篇论文FROM RANDOM POLYGON TO ELLIPSE: AN EIGENANALYSIS。这篇论文证明了,平面上任何一个多边形(可自交),不断取各边的中点重新连线,同时按比例放大,往复操作最终会趋近于一个椭圆。以下是一个例子的动态图:
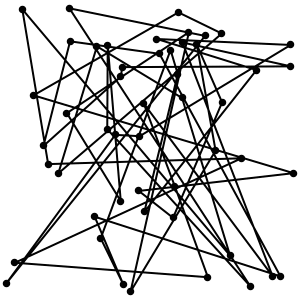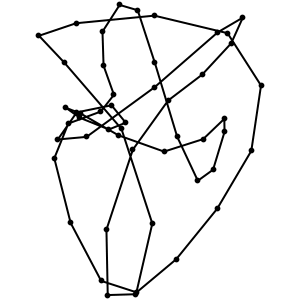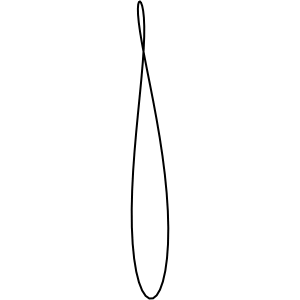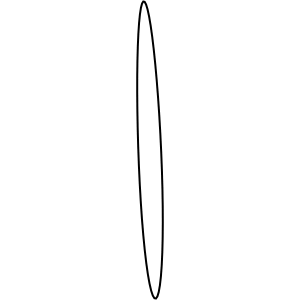
证明方法并不难,只用到一些线性代数的知识。如果不喜欢看英文,人人网的谢雨辰写了一篇减缩版的中文版证明。
线性代数的方法并未揭露出这个问题的本质。令人拍案叫绝的是,人人网的王赟从信号处理的角度,用傅立叶分析给该问题以新的解释,结论更直观(但需要事先了解所使用的数学方法)。而且,这种方法可以解决类似的问题,比如如果不是取中点而是用别的迭代方式会怎么样:
- 如果每次迭代是把每个顶点关于下一个顶点取镜像得到新的顶点,偶数各点时最终结果退化到两个点,奇数个点时最后收敛到一个刺猬。
- 如果每次迭代,是把相邻两个顶点的中点关于下一个顶点取镜像得到新顶点:当顶点个数为 7 的倍数而又不太多(如 14,21,28 )时,图形会收敛成一颗七角星。
甚至我们可以反过来设计什么样的迭代方式,能收敛到我们所想要的样子(比如五角星)。
上面线性代数和信号处理的思路都可以直接应用到三维的情况。在三维空间中,不断取重点最后也会收敛到一个椭圆。
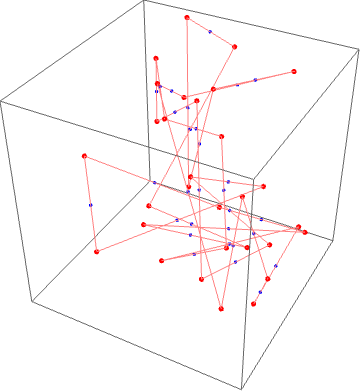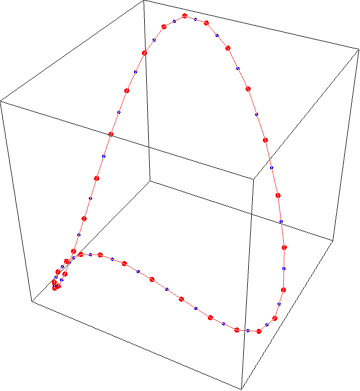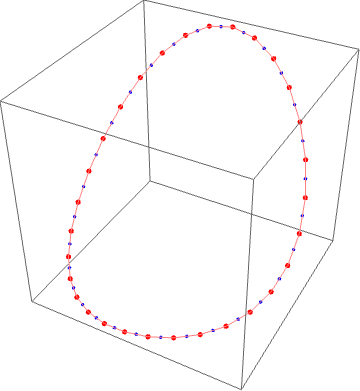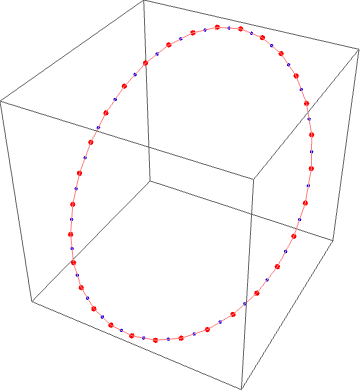
事情到这里还没完。人人网的张文琦在三维的情况上继续扩展。这时候考虑的是一个二维网格(首尾相连,最简单的例子是一个环面上均匀分布的经纬线行程的网格),每次迭代都是取每个方格的中心点形成一个新的二维网格。用数学公式表示:有$ n\times m$ 个顶点$ p_{i,j}$ ,$ 0\leq i < n$ ,$ 0\leq j < m$ 。$ n\times m$ 个面片$ T_{ij}$ 由$ p_{ij}, p_{i+1,j}, p_{i, j+1}, p_{i+1, j+1}$ 组成,其中$ p_{n, j} = p_{0,j}, p_{i,m}=p_{i,0}$ 。每一次的迭代都是取各个面片四个顶点的中心点形成新的网格,即
张文琦通过模拟发现,这种方法最后得到的是一个斜的椭圆形轮胎面。下面是一个例子的动态图:

这个具体是何原因还有待进一步探索。我觉得这个用上面信号处理的思路是可以做的,这个问题本质上还是点的变换(跟面其实没多大关系)。
2013-10-14 6:57PM 补充:
人人网的王赟已经用跟前面一样的滤波的方法,解决了上面问题。从滤波的角度看,最后留下来的是两个波的叠加,每个波都是一个椭圆。这样形成的曲面并不是张文琪所说的椭圆形轮胎面,而是一个 elliptic translational celestial。它是指一个椭圆沿着另外一个椭圆平行移动形成的曲面(一般说的环面则是一个圆绕着沿着另一个圆旋转移动形成的曲面,注意这里面的区别)。最后的结果长下面这个样子:
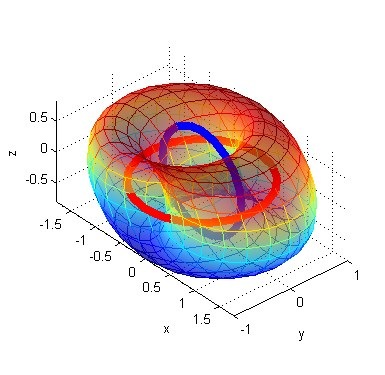
王赟的文章里有详细的分析,还提供了 Matlab 代码画图。有兴趣的可以移步观赏。
Q. E. D.
