overhang 堆积木 - 能伸出桌面多远？

作者: 张志强 , 2007-04-13 , 共 518 字 , 共阅读 0

来自University of Warwick的Mike Paterson星期二在 Yao 的理论计算机课堂上给了一个非常有趣的小讲座。

n 个长度为 1 的砖块，叠起来能伸出桌面多远？（只考虑方块各平面都与桌面平行的情况）。

下面这种放法，很多人高中学物理的时候都见过吧？它用 N 个砖块伸出了大约 $\ln(N)/2$ 。

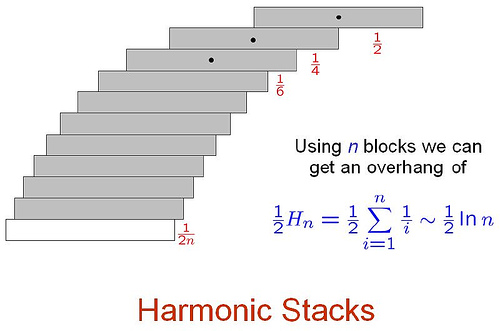
normal-method

上面这种叠放方法称为 Harmonic Stacks ，但它是最优的吗？下面这个例子可以看出，在 3 个砖块，我们就已经能做的更好了。

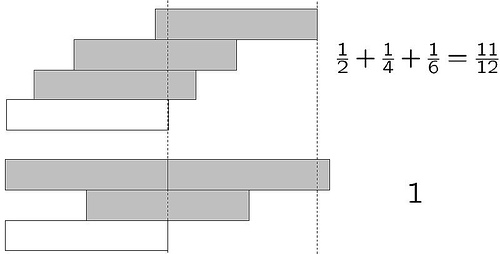
normal-method

上面这个能继续往上堆么？很不幸

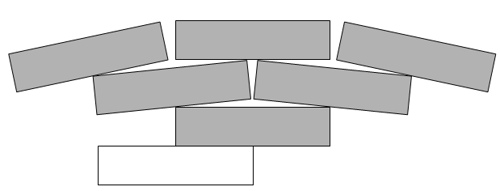
normal-method

下面这个也不行

往上叠也不行的

如果在上面再压很多砖块就可以了

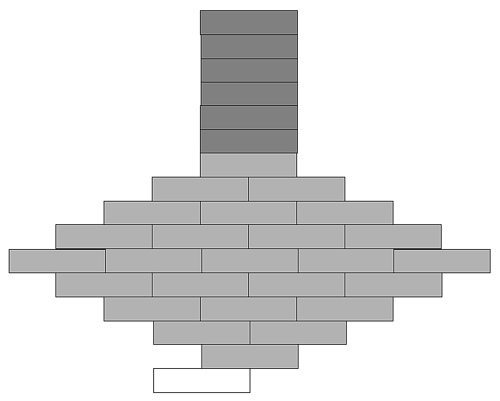
normal-method

下面是一种叠放方法，可以做到大约 $O(lnN)$ .

normal-method

但它也不是最优的，下面是 20 个和 30 个方块的最优叠放方法，它比上面的要好

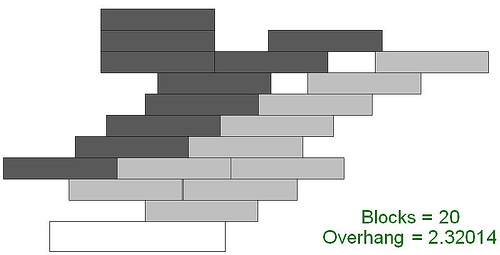
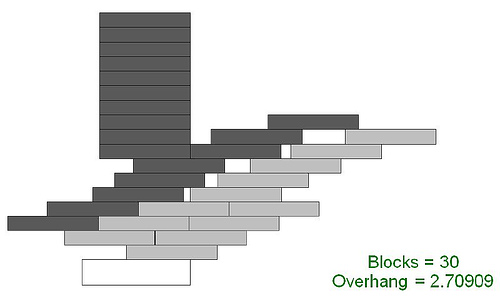
normal-method

下面是砖块数目比较少的时候的最优叠放方法。

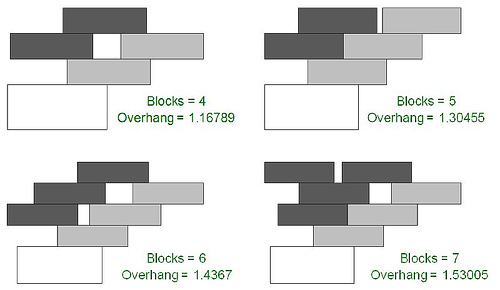
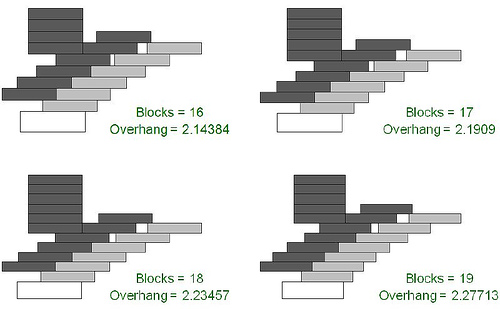
normal-method

不过说了这么多，上面的方法都只能做到 $ln(N)$ 的量级，而下面这个方法可以用 N 个砖块，往前伸出 $N^{\frac13}$ 的长度。

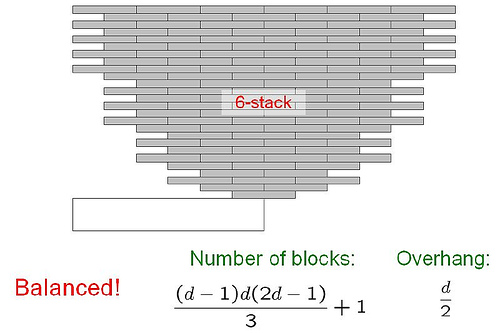
normal-method

而且，Mike Paterson及其合作者证明了，这种方法在量级上已经是最优的了！

Q. E. D.

本文将证明：最佳约会策略里提到策略，忽略前 37%的对象，然后在剩下的对象里挑第一个比前 37%都好的对象，这个策略是最优的。更准确地，我们将证明：任何约会策略的成功概率都不可能超过

$\frac{u}{n}\sum_{i=u}^{n-1}\frac1i$ ，其中

$u$ 为满足

$\sum_{i=u}^{n-1}\frac1i\geq 1$ 的最大值。这个

$u$ 大约为 37%，最后成功的概率大约为 40%。

以前提到过，理论计算机这门课会邀请一些正在这边访问的教授来讲课，由于是本科生，所以这些教授一般都是讲些有趣的东西，比如之前的overhang 堆积木 - 能伸出桌面多远？。今天这次课，来自 Aarhus 的Peter Bro Miltersen讲了一个很有趣的游戏问题。

这个问题有许多不同形式的阐述方式和变种，应用范围也很广。下面应该是比较吸引人和简单的那种，来自姚期智教授的理论计算机（ I ）的授课内容——我是其助教之一。