杀人的理论分析

作者: , 共 480 字 , 共阅读 0
系列：生活中的数学

查看该系列所有文章

「杀人」，英文名为"Mafia Game"，广泛流传于国内外。上个星期我们在玩的时候被Elchanan Mossel发现，然后他给了一个 talk ，内容就是杀人的理论分析。

他的论文在这里：Mafia : A Theoretical Study Of Players and Coalitions in a Partial Information Environment。

不过很可惜的是，国外和国内的游戏规则差别太大，比如他们玩游戏的时候每个人死了之后身份便会公开，这样便使得游戏的模型化成为可能，否则数学对对我们玩的个人心理站可无能为力。

在没有警察的游戏中，规则比较简单，有一个结论是杀手的数量应该是$ \sqrt{C}$ 量级的，大概是$ M=0.643\sqrt{C}$ 时，游戏才会平衡，其中 C 是平民数...不过这都要是 C 比较大的时候，否则怎么叫作"理论分析"呢 :)

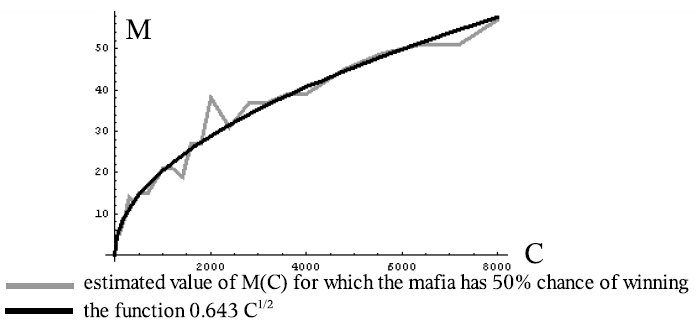
杀人游戏结果

但当有警察的时候，哪怕只有一个，杀手数需要和平民保持线形的关系，游戏才会平衡。

休息时间：来大斗智力吧，你选哪边？

扑克牌大战

Q. E. D.

系列： 生活中的数学 »
前一篇：
数学 » 心理学, 旁观者效应, 生活中的数学, 社会心理学, 纳什均衡
注：这篇文章是应 You XU 邀请的 guest blog。
后一篇：
数学 » 生活中的数学, 赌博
首先申明一下，赌博是不对的，下面的讨论也更多是理论性的。
类似文章：
相似度: 0.086
数学 » 数学游戏, 概率
《蚁迹寻踪及其他数学探索》提到一个游戏：
相似度: 0.072
数学 » 数学游戏, 脑筋急转弯
$ n$ 枚硬币排成一排，两人轮流取，每人每次可取其中一枚或者相邻的两枚。
相似度: 0.067
数学 » 生活中的数学, 赌博
在 slashdot 上看到一篇科技新闻，两个数学家（其中一个来自于 MIT ）和一个计算机学家，在 arXiv 上发表了一篇论文《HOW TO GAMBLE IF YOU』RE IN A HURRY》（PDF 版链接），是最近几天很热门的一条新闻。
相似度: 0.066
数学 » 石头剪头布, 纳什均衡, 生活中的数学, 数学游戏
这次去野外拓展，见到了一个比较好玩的划拳方式。与传统的石头剪刀布划拳一样，不过这里需要三轮：
相似度: 0.065
数学 » 头脑风暴, 数学游戏, 概率, 面试题
这个题目听说是 MSRA 的面试题。
相似度: 0.065
数学 » 悖论, 数学游戏, 赌博
一个游戏：持续的抛一个均匀硬币，直到抛到出现反面为止，假设在之前你抛除了$ k$ 次正面，你将得到$ 2^{k+1}$ 次方这么多钱。
相似度: 0.057
数学 » 脑筋急转弯, 数学游戏
Alice 和 Bob 两人玩一种硬币游戏。游戏在一个$ 2\times2$ 的棋盘上进行，棋盘上每个格子上都有一枚硬币。在每一回合， Alice 可以决定选择翻转某两枚或者一枚硬币，接着 Bob 可以选择将棋盘旋转 90 ， 180 或者 270 度，也可以什么都不做。
相似度: 0.054
数学 » 生活中的数学, 投资中的数学
注：来凑凑热闹，最先在槽边往事看到的，不过网上已经有相当多的讨论。
相似度: 0.052
数学 » 概率, 洗牌, 理论计算机课堂笔记, 生活中的数学
在大家玩牌的时候，每一局之前都需要重新洗牌——一次洗牌指将牌分为左右两垛然后穿插放牌，但多少次洗牌才是正当的呢？就我多次打牌的观察，多数人都不超过 4 次。
前一篇：
数学 » Rubik's Cube, 图论, 算法, 魔方
今天香港中文大学的Prof. Cai给我们上 graph algorithm。第一节课上教我们玩魔方，先给每人发了一个。我喜欢这样的教学方法 :) 。
后一篇：
数学 » open问题, 图论
孙博告诉我的，求证